Operations on Sets
Sets can be combined to form number of different sets.
The three basic operations on sets are:
1. Union of Sets
2. Intersection of Sets
3. Difference of Sets
Union of Sets
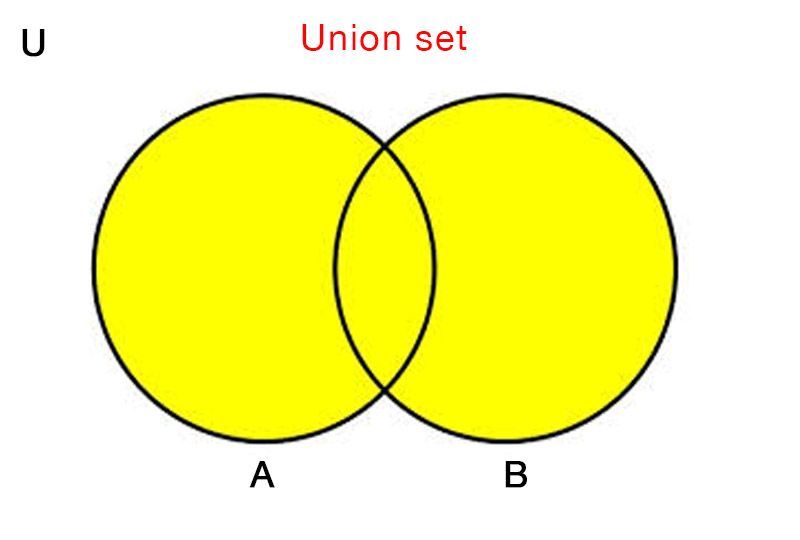
The union of set A and set B is denoted by A∪B .
It contains those elements that are either in set A or in set B, or in both.
Union of sets is commutative. i.e. A∪B = B∪A.
Set A and set B are subsets of A∪B. i.e. A ⊂ (A∪B) and B ⊂ (A∪B)
Intersection of Sets
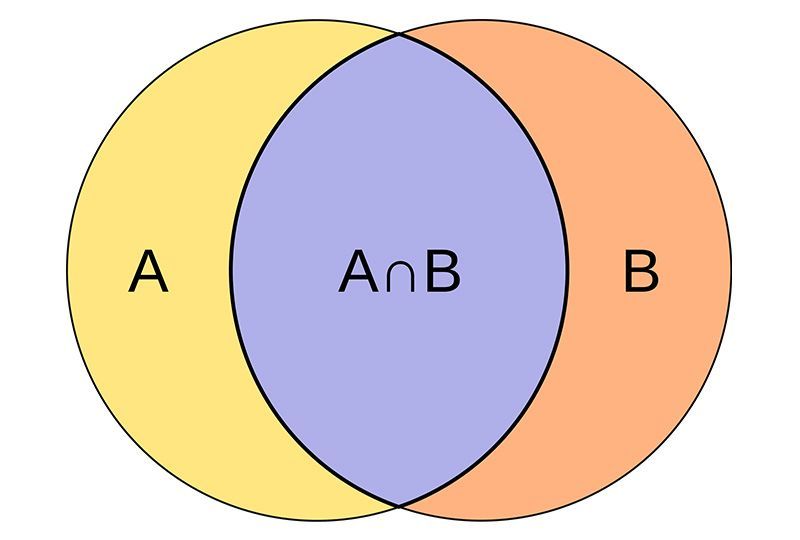
The intersection of two sets is a set containing all the elements which are both in set A and in set B.
The intersection of two sets A and B is denoted by A∩B. Intersection of sets is commutative.
A∩B is a subset of set A and set B. i.e. (A∩B) ⊂ A and (A∩B) ⊂ B.
If A and B are disjoint sets, then A∩B = ∅ (null set)
Difference of Sets
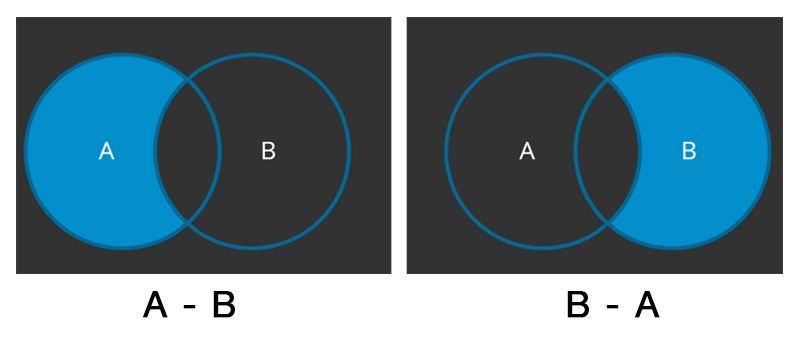
The difference of two sets (A - B) is the set containing only those elements which are in set A and not in set B.
The difference of two sets A and B is represented as (A-B).
Difference of sets is not commutative. A - B ≠ B - A.
Complement of Set
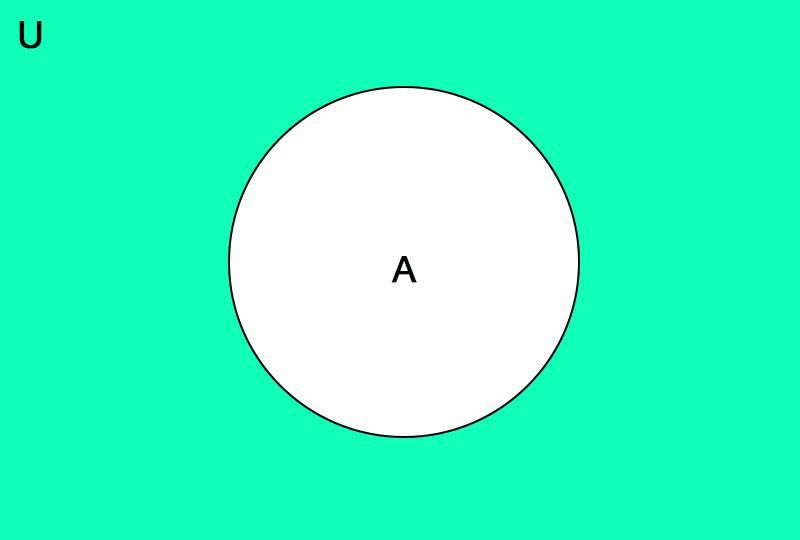
The difference of the universal set and a set A is called the complement of the set A.
It is denoted as A'.
Access All Content
Video Explanations, Practice Worksheets and Solved Examples for all Chapters.
Textbook solutions, Formulae and Mindmaps across all boards.
More from Grade 7 Math
Types of Lines
All you need to know about lines, parallel, perpendicular and intersecting lines. Along with all the examples from the world around you.
Types of Angles
Learn about the different types of angles acute, right, obtuse and more through exciting facts from the Wonders of the World.