Construction of Triangles.
To construct a triangle uniquely, we don't need to know all the 6 elements of the triangle.
A triangle of any size can be drawn if the given conditions are fulfilled.

The three sides of the triangle are given. SSS criterion
Two sides and the included angle are given. SAS criterion
One side and any two angles are given. AAS criterion
Two angles and including side is given. ASA criterion
Possibility of Construction
A triangle cannot be constructed if:
1. 3 angles are given. Since, the length of the sides can vary.
2. Two sides and non-included angle is given.
3. Sum of two sides should always be greater than third side.
SSS criterion
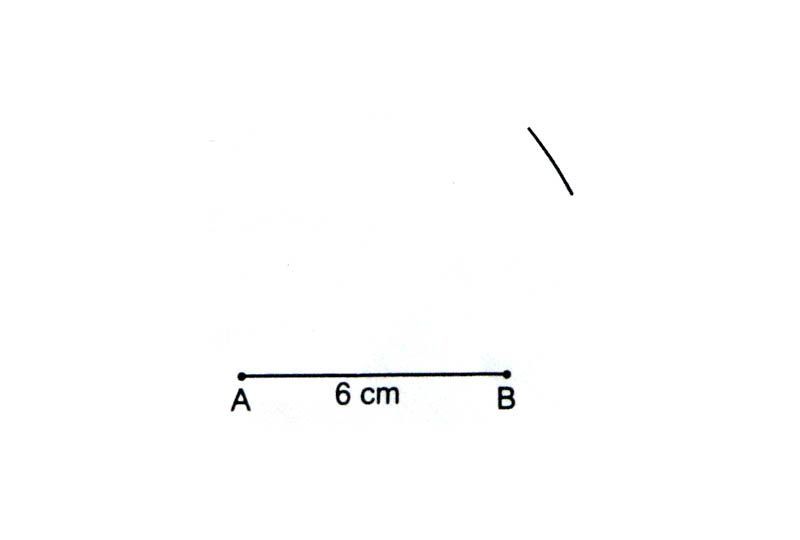
Draw a rough sketch of the triangle ABC.
Draw line segment AB = 6 cm.

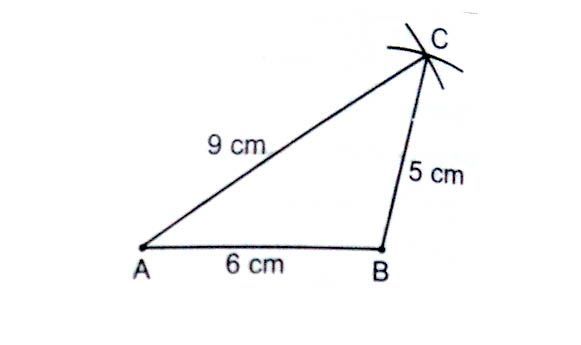
With A as centre and radius = AC = 9 cm. Draw an arc.
With B as the centre and radius = BC = 5 cm. Draw another arc to intersect the previous arc at point C.

Join A to C and B to C. Triangle ABC is the required triangle.
SAS criterion
Draw a rough sketch of the triangle PQR.
Draw line segment AB = 7 cm.

Using a protractor or a compass, construct angle of 60° at the point P.
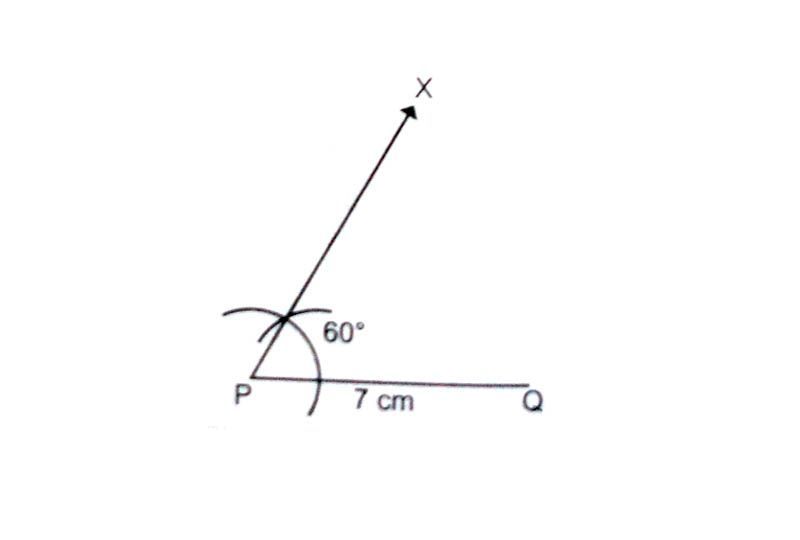
With P as the centre and radius = PR = 6 cm. Draw an arc to intersect XP at a point R.

Join RQ. Triangle PQR is the required triangle.

ASA criterion
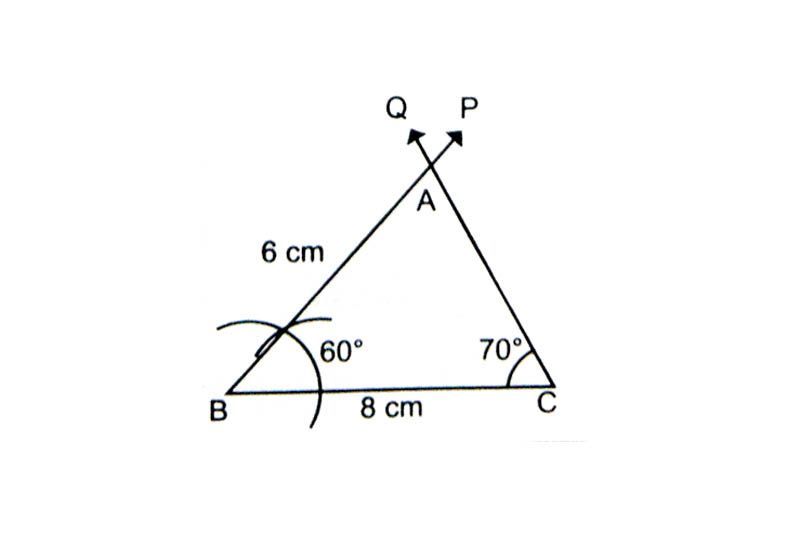
Draw a rough sketch of the triangle ABC.
Draw line segment BC = 8 cm.
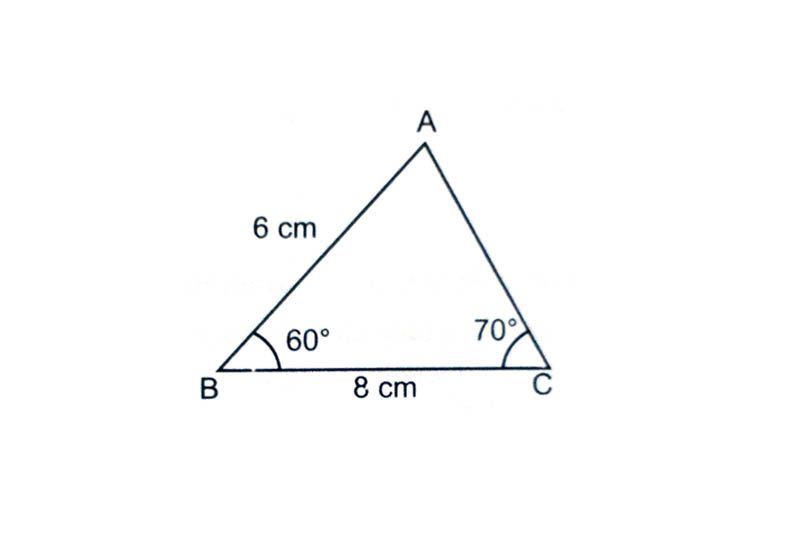
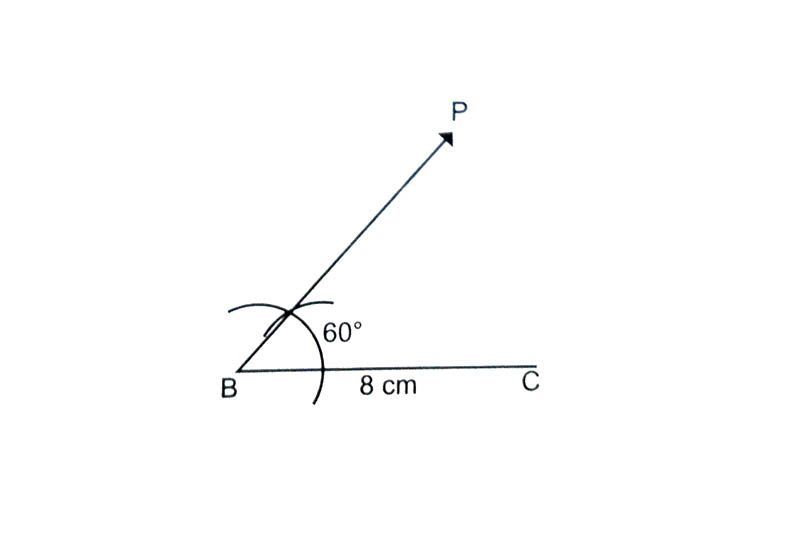
At B draw ∠PBC = 60° using a compass.
At C draw an ∠QCB = 70° using a protractor.
The point of intersection of PB and QC is the vertex A.
Triangle ABC is the required triangle.
Right Triangle
Draw a rough sketch of the triangle XYZ.
Draw line segment XY = 3 cm.
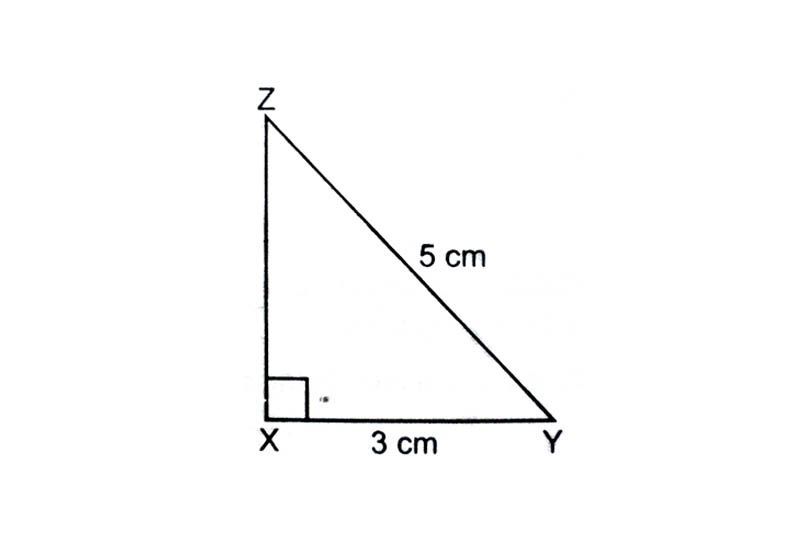
At X draw an ∠AXY = 90° using compass.
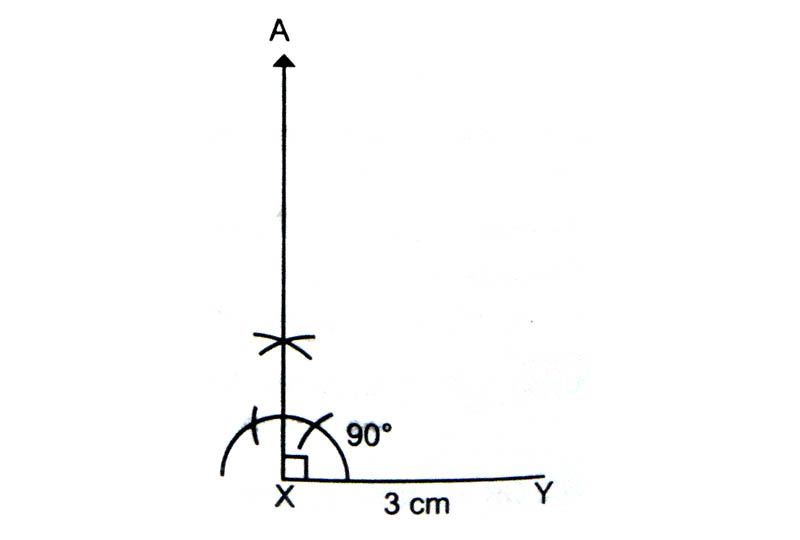
With Y as the centre and radius 5 cm. Draw an arc to intersect AX at Z.
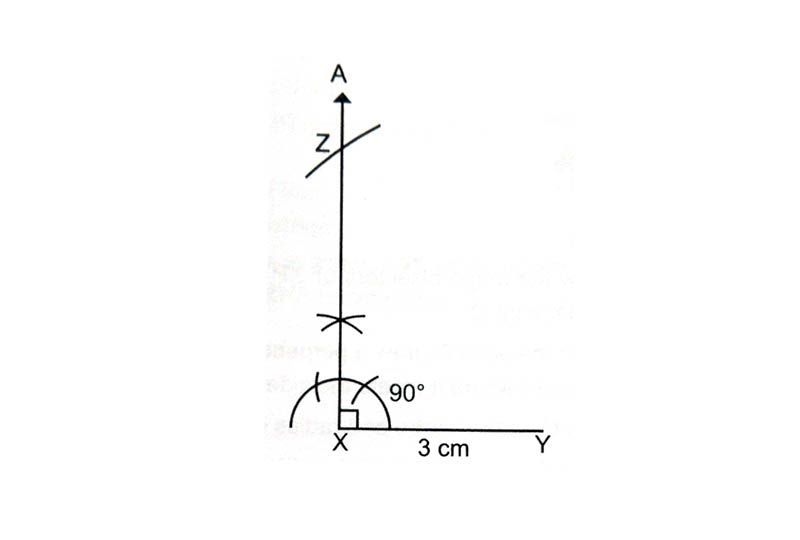
Join YZ. Triangle XYZ is the required triangle.