Operations on Sets
Sets can be combined to form number of different sets.
The three basic operations on sets are:
1. Union of Sets
2. Intersection of Sets
3. Difference of Sets
Union of Sets
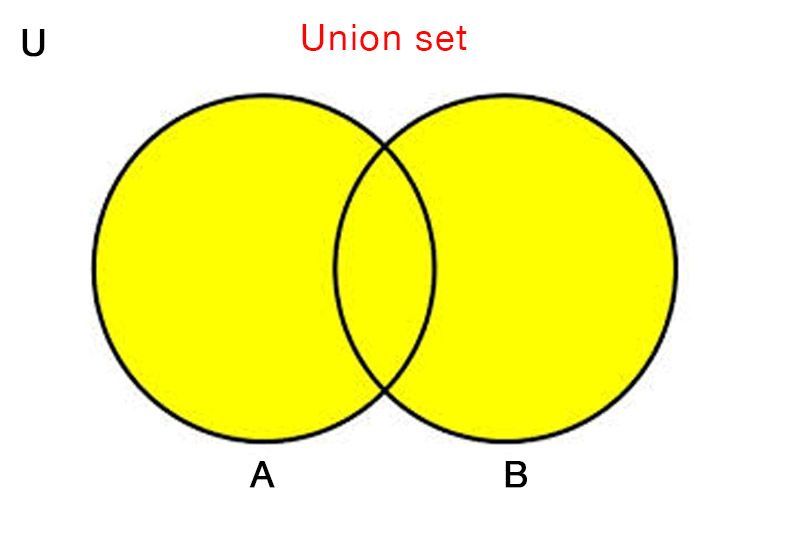
The union of set A and set B is denoted by A∪B .
It contains those elements that are either in set A or in set B, or in both.
Union of sets is commutative. i.e. A∪B = B∪A.
Set A and set B are subsets of A∪B. i.e. A ⊂ (A∪B) and B ⊂ (A∪B)
Intersection of Sets
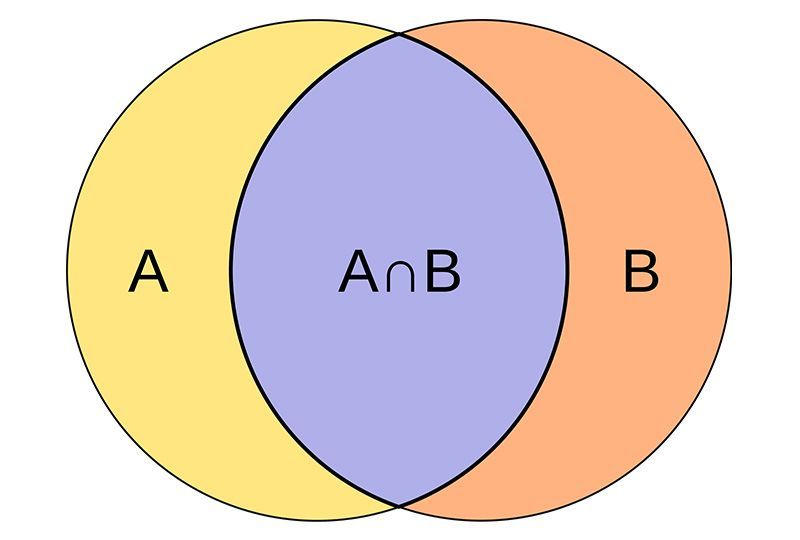
The intersection of two sets is a set containing all the elements which are both in set A and in set B.
The intersection of two sets A and B is denoted by A∩B. Intersection of sets is commutative.
A∩B is a subset of set A and set B. i.e. (A∩B) ⊂ A and (A∩B) ⊂ B.
If A and B are disjoint sets, then A∩B = ∅ (null set)
Difference of Sets
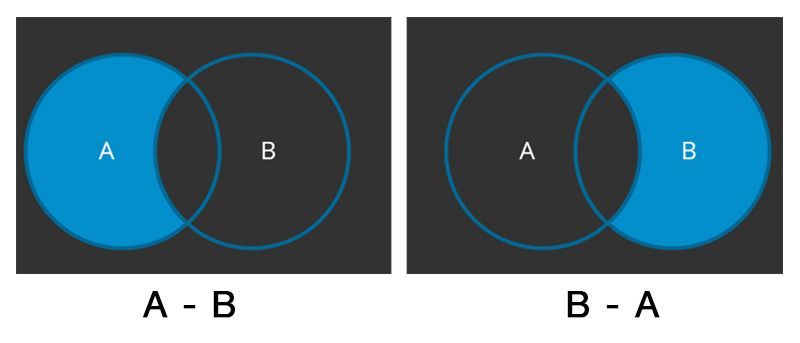
The difference of two sets (A - B) is the set containing only those elements which are in set A and not in set B.
The difference of two sets A and B is represented as (A-B).
Difference of sets is not commutative. A - B ≠ B - A.
Complement of Set
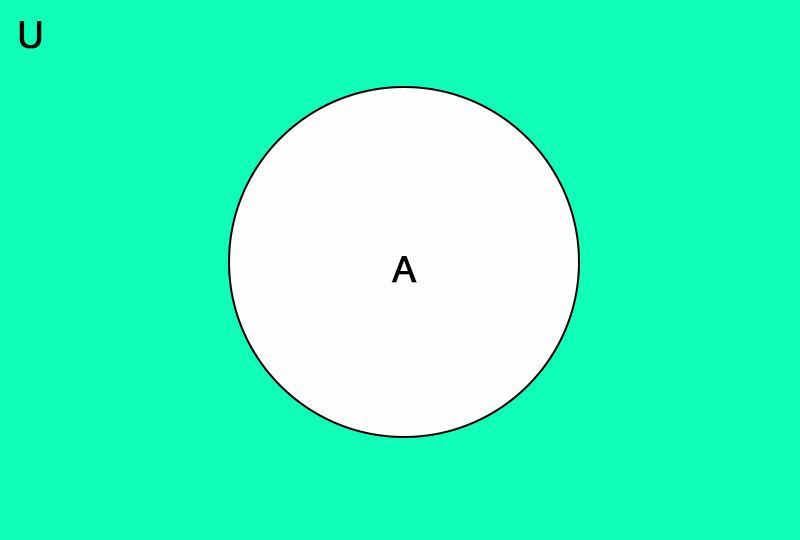
The difference of the universal set and a set A is called the complement of the set A.
It is denoted as A'.