Properties of Sets

Universal Sets
A set which contains all the sets under consideration is called the Universal set.
A rectangle is used to represent the universal set.
Subset
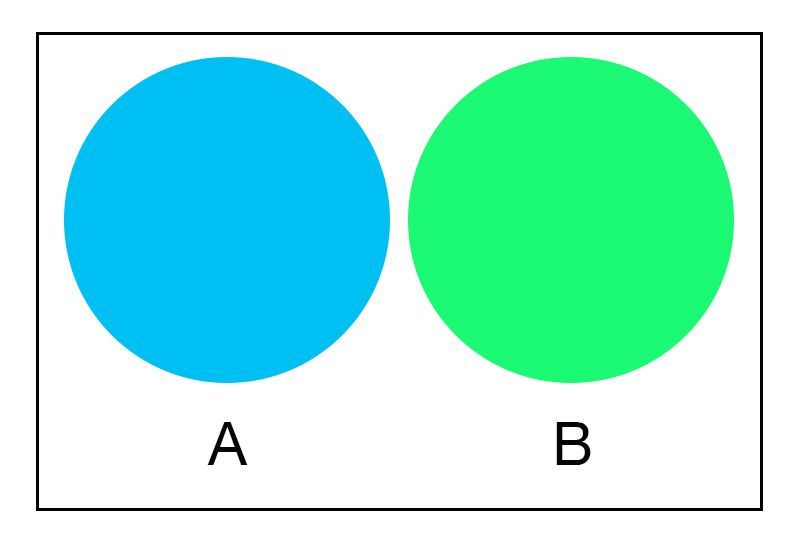
If every element of set A is in set B, then A is said to be the subset of B.
The symbol ⊆ is used to denote subset.
Superset
If A is a subset of B then we can say that B is the superset of A as it contains all the elements of A.
The symbol ⊇ is used to denote superset.
Proper Subset
Set A is said to be the proper subset of set B, if all the elements of set A are in set B and set B contains at least one extra element more, which is not in set A.
The symbol ⊂ is used to denote proper subset.
Number of Subsets
of a set
If a set has n elements then the number of subsets of the set will be 2n.
And the number of proper subsets will be 2n - 1
Empty Set
Every set is a subset of itself and an empty set is a subset of every set.
Power Set
The set containing all the possible subsets of a given set is called a power set.
The power set of a set S is denoted by P(S).
Complement of a set
The complement of set A is the set of all the elements which do not belong to A but belong to the universal set U.
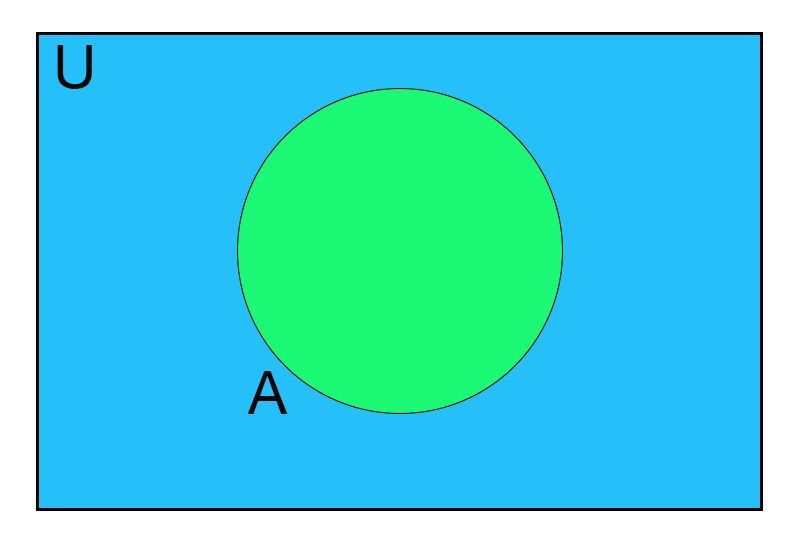
It is represented by A' (read as A complement).
Cardinal Properties
of Sets
For any two sets A and B.
n(A∪B) = n(A) + n(B) - n(A∩B)
n(A) + n(A') = n(U)
n(A∪B)' = n(U) - n(A∪B)
n(A∩B)' = n(U) - n(A∩B)
De Morgan's First Law.
(A∪B)' = A'∩B'
The complement of the union of two sets A and B is equal to the intersection of the complements.
De Morgan's Second Law.
(A∩B)' = A'∪B'
The complement of the intersection of the two sets A and B is equal to the union of the complements.